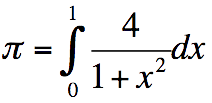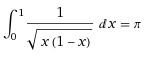| FN |
Utilities |
Examples |
| 1 |
Sound
Plays a short alert sound, defined by x (0..19).
Values outside this range will produce the standard beep sound.
|
x = 3 produces a series of three beeps.
x = 13 emits the sound used in "Merge Sound Control" (see next command)
x = 15 creates a pleasing sequence of piano tones. |
| –1 |
Merge Sound Control
When being prompted acoustically by a program to merge a card, this value specifies how many times the sound should be played. The default value is 3 times, but you can change this value using Merge Sound Control with the argument:
x = number of times to play the sound (0 for no sound)
Notes:
Merging a card on a real HP-67/97 could be automated by placing the card into the slot without pushing it in.
A soon as the sequence MERGE PAUSE was executed, the card would be pulled in, its code replacing everything after
the PAUSE command. The program would then continue at the first step of the merged card.
Since the RPN-67 and -97 simulators do not have a physical card slot, it's up to the user to provide the card to be merged from the Card Manager.
Executing a loop like:
LBL 0
MERGE
PAUSE
GTO 0
will wait for the user to load the card before continuing automatically. The loop alerts the user by a triple-beep sound to act,
issued as many times as specified by this command. If no card is provided by the user within 3 minutes, the merge command will be aborted.
A red bar is shown, indicating the time left until time-out occurs.
If the sound is suppressed by setting its repeat number to 0, no time-out will occur.
Note that the acoustic alert also works in vintage mode (available on the iPad), although the repeat number has to be defined in Enhanced Mode. |
For a sophisticated program involving two merge operations, see the program SIN or COS to 105 Places in the Math section of Library U. |
| 2 |
CLR EXT
Sets extended registers R.00..R.99 to 0.
|
|
| –2 |
CLR Flags
Clears all flags F0…F9.
|
To clear extended flags F4…F9 only, use operation CLR F4-F9 (no. 93, above) |
| 3 |
CLR STK
Sets stack registers X, Y, Z, T to 0.
|
|
| 4 |
CLR A..E
Sets registers A, B, C, D, E to 0.
|
|
| 5 |
PUSH A..E
Puts registers A..E on an internal 4-level stack.
If the stack is full, the oldest register set is lost.
|
|
| –5 |
POP A..E
Retrieves registers A..E from the internal 4-level stack.
The oldest level gets copied to the next level (like T to Z on the regular stack.)
|
|
| 6 |
REV STK
Reverses the order of stack registers X, Y, Z, T.
|
|
| 7 |
P ⇢ S
Copies primary registers to secondary registers (R0..R9 ➞ RS0..RS9).
|
|
| –7 |
P ⇠ S
Copies secondary to primary registers (RS0..RS9 ➞ R0..R9).
|
|
| 8 |
Separate x
Separates x into integer and fractional part.
On return: x = fractional part, y = integer part |
x = 3.141592654
EXEC FN ➞ x = 0.141592654, y = 3 |
| 9 |
Set +∞
Displays the positive overflow value 9.999999999 99 and lights the +∞ infinity symbol.
If executed from a running program, it will be halted.
|
TAN(90°) lights +∞ indicator.
If followed by N!, we get the factorial of infinity ∞! = √(2π) = 2.5066,
as a consequence of the derivative of the zeta function at 0 equalling log(√(1/2π)). |
| –9 |
Set -∞
Displays the negative overflow value -9.999999999 99 and lights the -∞ infinity symbol.
If executed from a running program, it will be halted.
|
|
| 10 |
RCL Extended ∑ Registers
Recalls extended statistical registers used internally for weighted mean,
T-statistics, skewness, and kurtosis to the stack.
The previous x-value is saved in LastX.
|
x = ∑x2 , y = ∑(x-y)2y , z = ∑x3y , t = ∑x4
|
| 11 |
P ≷ Non-Stat
Swaps primary and non-statistical registers (R0..R3).
|
Exchanges R0..R3 with RS0..RS3.
|
| –11 |
P ≷ Stat
Swaps primary and statistical registers (R4..R9).
|
Exchanges R4..R9 with RS4..RS9.
|
| 12 |
STK & A..E ⇢ R.00..R.08
Copies stack and registers A..E to extended registers R.00..R.08.
|
|
| –12 |
STK & A..E ⇠ R.00..R.08
Retrieves stack and registers A..E from extended registers R.00..R.08.
The previous x-value is saved in LastX.
|
|
| 13 |
PUSH Registers
Puts primary registers R0..R9 and secondary registers RS0..RS9 on an internal 4-level stack.
If the stack is full, the oldest register set is lost.
|
|
| –13 |
POP Registers
Retrieves registers R0..R9 and secondary registers RS0..RS9 from the internal 4-level stack.
The oldest level gets copied to the next level (like T to Z on the regular stack.)
|
|
| 14 |
Save Warnings on
In Card Manager, enables warnings when trying to leave the current card with unsaved changes.
|
|
| –14 |
Save Warnings off
In Card Manager, suppresses warnings when trying to leave the current card with unsaved changes. |
|
| 15 |
CPLX Mode on
Turns complex mode on. Same as h A or EXT A when complex mode is off. |
|
| –15 |
CPLX Mode off
Turns complex mode on. Same as h A or EXT A when complex mode is on. |
|
| 16 |
Toggle CPLX Mode
Turns on complex mode, if it is currently off, and vice versa.
|
This command is useful in cases where the stack has already been set up with complex arguments.
Conversely, the extended operation CPX MODE (01, see above) requires x to define the desired setting, disrupting the stack.
|
| 17 |
Get Haptics
Retrieves the current haptic feedback level, where:
-1 = device doesn't support haptics
0 = no feedback | 1 = light | 2 = medium | 3 = heavy
|
|
| –17 |
Set Haptics
Sets the current haptic feedback level, where:
0 = no feedback | 1 = light | 2 = medium | 3 = heavy
Other values are ignored.
|
This command does nothing if:
– the device does not support haptic feedback
– the iOS version is less than 10
– System Haptics have been turned off in the device settings
|
| 20 |
Print Date
Prints the localized date on the paper tape (right-justified).
x = date (mm.ddyyyy). If invalid, the current date is used.
|
Print the current date (Nov 20, 2017, USA)
0 EXEC FN → November 20, 2017
Print Oct 23, 1956 (Hungary)
10.231956 EXEC FN → 1956. október 23.
|
| -20 |
Print Time
Prints the localized time on the paper tape (right-justified).
x = time (hh.mmss). If invalid, the current time is used.
Fractions of seconds are ignored.
|
Print the current time (15:01:25, USA)
-1 EXEC FN → 3:01:25 PM
Print 15:01:25 (Finland)
15.0125 EXEC FN → 15.01.25
|
| 21 |
Print DOW
Prints the localized name of the day of week of the given date on the paper tape (right-justified).
x = date (mm.ddyyyy). If invalid, the current date is used.
Use negative date for Julian calendar.
Weekdays up to and including Oct 14, 1582 are Julian by default.
If the date is an Easter date, "Sunday" is replaced by "Easter".
|
Print the day of the week of Isaac Newton's birth
1.041643 EXEC FN → Sunday (Gregorian calendar)
-12.251642 EXEC FN → Sunday (Julian calendar)
Print the day of the week of Isaac Newton's death (on Polish iOS device)
3.311726 EXEC FN → niedziela (Sunday, Gregorian calendar, old style)
-3.201726 EXEC FN → niedziela (Sunday, Julian calendar)
|
| 22 |
Print Device Name
Prints the name of the device the app is running on.
Returns in x the type of device:
1 = iPhone, 2 = iPad, 3 = iPod, 0 = other (negative if running on Apple Silicon Mac).
NOTE: On a Mac, the system currently returns "iPad" for all devices.
|
If executed on an iPad Pro running iOS 10.3.3:
EXEC FN → prints iPad on printer
Display = 2 (for iPad)
|
| -22 |
Print iOS Version
Prints the iOS version number.
Returns in x the version as numeric value.
|
If executed on a device running iOS 10.3.3:
EXEC FN → prints iOS 10.3.3 on printer
Display = 10.33
|
| 25 |
Print Inline Text 1
Prepends the next line to be printed with pre-defined text.
x = number of extended register where text begins
(see operation TEXT, no. 87, above for details)
A PDF list of possible TEXT characters may be downloaded here.
|
To print a result prepended by α–β:
Assuming the text is stored in registers R.80 and R.81:
0.192045193 STO.80 "α–β"
0.058000000 STO.81 ":" (Note that a 000-value ends the string)
80 EXEC FN → text at R.80 is ready for printing
Print text,
e.g. result 152.75 → α-β: 152.75 *** |
| –25 |
Print Inline Text 2
Same as Print Inline Text 1, but with the result indicator " ***" suppressed,
providing more space for the user text.
Note:
If x points to a register containing 0, the user text is also suppressed.
|
To print a result prepended by α–β:
Assuming the text is stored in registers R.80 and R.81:
0.192045193 STO.80 "α–β"
0.058000000 STO.81 ":" (Note that a 000-value ends the string)
80 EXEC FN → text at R.80 is ready for printing
Print text,
e.g. result 152.75 → α-β: 152.75
|
| 26 |
Print Line Pattern
Prints any of 14 line patterns on the paper tape.
x = pattern number (1..14)
If x is invalid, an empty line will be printed.
1: ––––––––––– 8: - - - - - -
2: =========== 9: = = = = = =
3: -=-=-=-=-=- 10: -+-+-+-+-+-
4: *********** 11: * * * * * *
5: /\/\/\/\/\/ 12: ‗‗‗‗‗‗‗‗‗‗‗
6: ——————————— 13: ▬▬▬▬▬▬▬▬▬▬▬
7: ∙∙∙∙∙∙∙∙∙∙∙ 14: ● ● ● ● ● ●
Note:
The patterns are the same as made available on RPN-67/97 Pro by tapping TXT.
In TXT, patterns are numbered 1..7 in the left column, 8..14 in the right column.
|
To print a solid line:
6 EXEC FN
To print a thick solid line:
13 EXEC FN
To print a double line:
12 EXEC FN
|
| 30 |
Load Data Card
Loads the data card named zDATAx, where x is any integer between 0 and 1,000,000 (sign and fractional digits ignored).
All data on the card gets loaded, i.e. primary and secondary registers as well as extended registers 00..99.
The command returns:
• the number of cards named zDATAx found (only the first will get loaded)
(0 if the specified data card does not exist)
• –1 if an error occurred
The card number is saved in LastX.
Working with zDATA data cards sample programs: 
|
If embedded in an auto-executing subroutine (LBL 99), registers may be preloaded without using program code and without user intervention.
For example:
90 99 LBL 99
"+30"
33 43 STO FN
"+123"
32 44 99 OP EXEC FN
35 22 RTN
would auto-load all registers from the data card zDATA123.
(Note: How to enter values like "+123" is shown in OP 98 above).
|
| –30 |
Load Data Card Ext
Loads only the extended registers from the data card named zDATAx (where x is any integer between 0 and 1,000,000, sign and fractional digits ignored).
Stack registers Y and Z contain the range of registers to load. Each value is automatically limited to the range 0..99.
Stack register T may specifiy the register to receive the first value of the range. If invalid, the range will be stored at the original location.
The command returns:
• the number of cards named zDATAx found (only the first will get loaded)
(0 if the specified data card does not exist)
• –1 if an error occurred
The card number is saved in LastX.
|
Example:
"-30"
33 43 STO FN
"+20"
41 ENTER
"+75"
41 ENTER
"+85"
41 ENTER
"+123"
32 44 99 OP EXEC FN
would load registers R.75..R.85 from the data card zDATA123 beginning at R.20.
(Note: How to enter values like "+123" is shown in OP 98 above).
|
| 31 |
Create or Update Data Card
Stores all registers on the data card(s) named zDATAx (where x is any integer between 0 and 1,000,000, sign and fractional digits ignored).
If the card already exists, it will be updated (unless it is write-protected.)
The command returns:
• 0 if at least one card named zDATAx was updated
• 1 if a card named zDATAx was created
• –1 if the operation failed
• –2 if all cards zDATAx are write-protected
The card number is saved in LastX.
Note:
As a safeguard against programming errors, card creation is limited to 100 cards per second. If exceeded, the program will stop with "Error".
|
Example:
"+31"
33 43 STO FN
"+123"
32 44 99 OP EXEC FN
would create (or update) the data card zDATA123.
(Note: How to enter values like "+123" is shown in OP 98 above).
|
| –31 |
Delete All Data Cards
Deletes all unprotected data cards whose name begins with zDATA (matching letter-case.)
x must be set to 666, otherwise the command is ignored.
The command returns:
• the number of data cards beginning with zDATA deleted
• –1 if the operation failed
|
Example:
"-31"
33 43 STO FN
"+666"
32 44 99 OP EXEC FN
would delete all unprotected data cards beginning with zDATA.
(Note: How to enter values like "+123" is shown in OP 98 above).
|
| 32 |
Delete Data Card
Deletes all unprotected data cards named zDATAx (where x is any integer between 0 and 1,000,000.)
The command returns:
• the number of data cards named zDATAx deleted
• –1 if no card named zDATAx was found
• –2 if all cards named zDATAx are write-protected
|
Example:
"+32"
33 43 STO FN
"+123"
32 44 99 OP EXEC FN
would delete the unprotected data cards named zDATA123.
(Note: How to enter values like "+123" is shown in OP 98 above).
|
| –32 |
Delete Data Card Series
Deletes y unprotected data cards named zDATAx, zDATAx+1, zDATAx+2, .. zDATAx+y-1
(where x is any integer between 0 and 1,000,000-y+1.)
y must be in the range 1..100.
Returns the number of data cards deleted
|
Example:
"-32"
33 43 STO FN
"25"
41 ENTER
"+123"
32 44 99 OP EXEC FN
would delete data cards named zDATA123, zDATA124, zDATA125 up to
zDATA146, leaving protected cards intact.
|
| 33 |
Check Data Card Existence I
Checks if a data card named zDATAx exists (where x is any integer between 0 and 1,000,000.)
If the card does not exist, the program stops and "zDATAx missing" is printed on the paper tape.
The command returns:
• the number of data cards named zDATAx found, –2 if none
• –1 if the operation failed
The card number is saved in LastX.
|
Example:
"+33"
33 43 STO FN
"+796314"
32 44 99 OP EXEC FN
would return –2 if no data card named zDATA796314 exists.
"zDATA796314 missing" would be printed, and the program would stop.
If three cards of this name were found, the value 3 would be returned.
(Note: How to enter values like "+796314" is shown in OP 98 above).
|
| –33 |
Check Data Card Existence II
Checks if a data card named zDATAx exists (where x is any integer between 0 and 1,000,000.)
This command works the same as #33 above, except that:
– The program does not stop if the card is not found
– The message "zDATAx missing" is only printed in print modes NORM and TRACE.
|
|
| 40 |
MAT MOD
Modifies registers R1…R9 (frequently used to store an up to 3x3 matrix) by applying a predefined operation to each register.
x = number defining the desired operation (see below)
y = argument (required by dyadic operations)
Dyadic operations applied to each register, argument in y:
1 -
2 +
3 ×
4 / Error if y = 0
5 ^ Error if reg = 0 and y ≤ 0; or
reg < 0 and y or 1/y not integer
Monadic operations applied to each register:
10 √x Error if any register < 0.
11 x²
12 LN Cleared registers ignored.
Error if any register < 0.
13 eˣ
14 LOG Cleared registers ignored.
Error if any register < 0.
15 10ˣ
16 1/x Cleared registers ignored
17 CHS
18 ABS
19 INT
20 FRAC
21 RND Round according to display settings
22 RAN# Random number (0 ≤ r < 1)
Miscellaneous operations
23 SORT Sort registers in ascending (y pos.) or
descending (y neg.) order.
If y = ±1…9, only the first y registers
are sorted.
24 DUPS Check for duplicates in R1…R9.
Returns 0 if no duplicates were found,
1 otherwise.
If y = 2…9, only the first y registers
are checked.
|
To invert every register from R1 to R9:
16 EXEC FN
Note how registers containing 0 are simply skipped; no error is produced.
To convert every register from R1 to R9 to its square root:
10 EXEC FN
If any of the registers is negative, an error is produced. None of the registers will be changed.
To make sure every register from R1 to R9 is negative:
18 EXEC FN 17 EXEC FN
This first makes the registers positive, then changes their signs.
To divide every register from R1 to R9 by 2:
2 ENTER 4 EXEC FN
To take the cube root of every register from R1 to R9:
3 1/x 5 EXEC FN
To create nine sorted random integers in the range 0...99:
22 EXEC FN EEX 2 ENTER 3 EXEC FN 19 EXEC FN 23 EXEC FN
To check if there are duplicates in R1..R6:
6 ENTER 24 EXEC FN
|
| 80 |
Change Info Display (RPN-97 only)
Sets the info shown above the display according to x:
0 = none
1 = registers
2 = instructions
3 = program code
|
This command is ignored on RPN-67. |
| 90 |
GTO (j)
Continues program execution at the label stored in J (where 0 ≤ j ≤ 99).
|
To use GTO (j) without affecting the stack, use an auxiliary subroutine, e.g.:
90 90 LBL 90
35 14 PUSH STACK
"+90"
33 43 STO FN
35 15 POP STACK
32 44 99 OP EXEC FN
35 22 RTN
Then, after setting j, simply use GTO 90 to branch to label j. |
| –90 |
GSB (j)
Calls the subroutine at the label stored in J (where 0 ≤ j ≤ 99).
|
To use GSB (j) without affecting the stack, use the same auxiliary subroutine as shown above.
Then, after setting j, simply use GSB 90 to call subroutine j. |
| 91 |
STO J
Stores the positive integer part of x in the indirection register J.
Values equal or larger than 100 are ignored.
|
|
| –91 |
RCL J
Recalls the indirection register J value to x.
|
|
| 92 |
INC J
Increases the value of the indirection register J by one. Ignored if j = 99.
|
|
| –92 |
DEC J
Decreases the value of the indirection register J by one. Ignored if j = 0.
|
|
| 93 |
GTO (k)
Continues program execution at the label stored in K (where 0 ≤ k ≤ 99).
|
To use GTO (k) without affecting the stack, use an auxiliary subroutine, e.g.:
90 91 LBL 91
35 14 PUSH STACK
"+93"
33 43 STO FN
35 15 POP STACK
32 44 99 OP EXEC FN
35 22 RTN
Then, after setting k, simply use GTO 91 to branch to label k.
|
| –93 |
GSB (k)
Calls the subroutine at the label stored in K (where 0 ≤ k ≤ 99).
|
To use GSB (k) without affecting the stack, use the same auxiliary subroutine as shown above.
Then, after setting k, simply use GSB 91 to call subroutine k. |
| 94 |
STO K
Stores the positive integer part of x in the indirection register K.
Values equal or larger than 100 are ignored.
|
|
| –94 |
RCL K
Recalls the indirection register K value to x.
|
|
| 95 |
INC K
Increases the value of the indirection register K by one. Ignored if k = 99.
|
|
| –95 |
DEC K
Decreases the value of the indirection register K by one. Ignored if k = 0.
|
|
| 96 |
Auto-exec Sound
Turns sound on loading auto-executing program card off or on.
x = 0: turn sound off
x ≠ 0: turn sound on
|
|
| 97 |
Get Pause
Retrieves the currently set pause length (in secs).
|
|
| –97 |
Set Pause
Sets the pause length.
x = 1, 2, or 5 (seconds). Other values are ignored.
|
|
| 98 |
Get Volume
Retrieves the currently set sound volume (any value between 0 and 1).
|
|
| –98 |
Set Volume
Sets the sound volume.
x = any value between 0 and 1. Values outside this range are ignored.
|
|
| 99 |
Save Calculator Settings
Stores the current display mode, trig mode, DP character, and group separator.
|
|
| –99 |
Restore Calculator Settings
Restores the saved display mode, trig mode, DP char, and group separator.
Ignored if no settings have been saved beforehand.
|
|
| |
Math |
|
| 100 |
Numerical Integration
Finds value of integrating a function f(x) over a given range.
The function f(x) may expect the stack to be filled with x.
x = label where function f(x)is stored
y = upper limit, z = lower limit
Label can be:
LBL 0 – 9: 0 – 9
LBL A – E: 11 – 15
LBL a – e: 11.1 – 15.1
LBL 00 – 99: 0 – 99 (append .2 for 00 – 09 and 11 – 15)
|
1) Show that
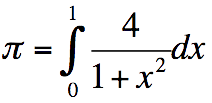
Store the function as LBL.67 (in W/PRGM mode):
LBL + 67 x2 1 + 4 ÷ 1/x RTN
Switch back to RUN mode.
Enter range and label:
0 ENTER 1 ENTER 67 EXEC FN → 3.141592654
2) Integrate f(x) = xx between 0 and 1
Use LBL A to store the function (in W/PRGM mode):
LBL A yx RTN
Switch back to RUN mode.
Enter range and label:
0 ENTER 1 ENTER 11 EXEC FN → 0.7834305107
If you want to evaluate the function manually, be sure to fill the entire stack with the argument x before executing the subroutine (unless the function doesn't make use of this.)
|
| –100 |
Integration Accuracy
Selects the accuracy of the Numerical Integration function, trading precision with speed of execution.
In most cases, the setting "Normal" will produce results with at least display precision.
x = accuracy value
Values (other values select the default setting "Normal"):
0: Normal
1: High
2: Best |
Computing the following integral which evaluates to infinity at both ends of the interval:
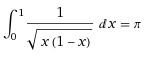
yields the following results:
3.134803651 Normal
3.138194839 High
3.139892917 Best
|
| 101 |
Find Root
Finds roots of a function f(x) in a given range.
If no root can be found, 0 is returned and flag F9 is set. If F9 is cleared, 0 is a solution.
The function f(x) may expect the stack to be filled with x.
x = label where function f(x) is stored
y = upper guess, z = lower guess
Label can be:
LBL 0 – 9: 0 – 9
LBL A – E: 11 – 15
LBL a – e: 11.1 – 15.1
LBL 00 – 99: 0 – 99 (append .2 for 00 – 09 and 11 – 15)
|
Solve ex2+7x-30 = 1
Use LBL 1 to store the function (in W/PRGM mode):
LBL 1 x2 x≷y 7 × + 30 – ex 1 – RTN
Switch back to RUN mode.
Try range 0..20:
0 ENTER 20 ENTER 1 EXEC FN → 3 (exactly)
Try range -20..0:
-20 ENTER 0 ENTER 1 EXEC FN → -10 (exactly)
If you want to evaluate the function manually, be sure to fill the entire stack with the argument x before
executing the subroutine (unless the function doesn't make use of this.)
|
| 102 |
Runge-Kutta 1
Finds solution of a first-order ordinary differential equation by applying the explicit fourth-order Runge-Kutta method.
In other words, the method finds function values of y(x) where only the slope (derivative) y'(x) at any point (x,y) is defined by a function f(x,y),
but y(x) is unknown. Since an infinite number of functions meet this requirement, a starting point (x0,y0) satisfying y0 = y(x0) has to be given.
By taking into account the slope y' = f(x,y) at this point, then increasing x by an increment h, successive points
of y(x) are found. The calculation ends when x0 + n × increment (n integer) exceeds the desired x value.
The user-supplied function f(x,y) determining the slope at (x,y) may expect the stack to be preset with x,y in X,Y as well as in Z,T.
Input:
Register A = label where function f(x,y) is stored *)
Register B = increment h between x values
Register C = x-value of starting point x0
Register D = y-value of starting point y0
x = x-value at which y(x) is to be found
Output:
x = x-value of function value y(x), i.e. the first value x0 + n × increment
exceeding the desired x-value
y = function value y(x)
*)
Label can be:
LBL 0 – 9: 0 – 9
LBL A – E: 11 – 15
LBL a – e: 11.1 – 15.1
LBL 00 – 99: 0 – 99 (append .2 for 00 – 09 and 11 – 15)
Note:
If flag F9 is set, the increment h will be automatically adjusted, if necessary, to maintain accuracy.
|
1) Solve at x = 1: y' = y, with x0 = 0, y0 = y(0) = 1
y' = y has an exact solution: y = ex + C (C = any constant).
By choosing the starting point (0,e0=1), we should get the function y(x) = ex and thus y(1) = e = 2.71828.
Since y' = y, the function f(x,y) for calculating the slope simply has to return y.
Use LBL 9 to store the function (in W/PRGM mode):
LBL 9 x≷y RTN
Switch back to RUN mode.
Store the label number in register A:
9 STO A
Enter arguments (increment h = 0.1, starting point, x):
0.1 STO B 0 STO C 1 STO D 1
Execute:
EXEC FN → x = 1, y = 2.718279744 (≈ e)
The slope of y = ex at (1,e) is e.
Check accuracy:
ex %CH → correct result is 0.000077% higher
Find e2.66, using h = 0.01 :
0.01 STO B 2.66
Execute:
EXEC FN → x = 2.66, y = 14.2962891
Check accuracy:
ex %CH → correct result is 0.000000022% higher
2) Solve at x = 1.5: y' + 0.7y = 2x, with x0 = 0, y0 = y(0) = -20/4.9
The function to store is y' = 2x - 0.7y
We use LBL 8 (in W/PRGM mode):
LBL 8 2 × x≷y 0.7 × – RTN
Switch back to RUN mode.
Store the label number in register 0:
8 STO A
Enter arguments (starting point, increment h = 0.1, x):
0.1 STO B 0 STO C 20 ENTER 4.9 ÷ CHS STO D 1.5
Execute:
EXEC FN → x = 1.5, y = 0.204081633
[Note: y(x) = 20/4.9*(0.7x-1)]
|
| –102 |
Runge-Kutta 2
Finds solution of a second-order ordinary differential equation by applying the explicit fourth-order Runge-Kutta method.
In other words, the method finds function values of y(x) where only the second derivative y"(x) at any point (x,y) is defined by a function f(x,y,y'),
but y(x) is unknown. Since an infinite number of functions meet this requirement, a starting point (x0,y0,y0')
satisfying y0 = y(x0) and y0' = y'(x0) has to be given.
By taking into account the second derivative y" = f(x,y,y') at this point, then increasing x by an increment h, successive points
of y(x) are found. The calculation ends when x0 + n × increment (n integer) exceeds the desired x value.
The user-supplied function f(x,y,y') determining the second derivative at (x,y) may expect the stack to be preset with x,y,y' in X,Y,Z, respectively.
Input:
Register A = label where function f(x,y,y') is stored *)
Register B = increment h between x values
Register C = x-value of starting point x0
Register D = y-value of starting point y0
Register E = y'-value at starting point x0,y0
x = x-value at which y(x) is to be found
Output:
x = x-value of function value y(x), i.e. the first value x0 + n × increment
exceeding the desired x-value
y = function value y(x)
*)
Label can be:
LBL 0 – 9: 0 – 9
LBL A – E: 11 – 15
LBL a – e: 11.1 – 15.1
LBL 00 – 99: 0 – 99 (append .2 for 00 – 09 and 11 – 15)
Note:
If flag F9 is set, the increment h will be automatically adjusted, if necessary, to maintain accuracy.
|
Solve at x = 0.9:
(1 – x²) y" + xy' = x, with x0 = 0, y0 = y(0) = 0, y0' = y'(0,0) = 0
The function to store is y" = x(1 – y') / (1 – x2)
Use LBL a to store the function (in W/PRGM mode):
LBL a RCL – . T x≷y × LASTx x2 1 – ÷ CHS RTN
Switch back to RUN mode.
Store the label name in register A:
11.1 STO A
Store arguments (increment h = 0.1, starting point, y0', x):
0.1 STO B 0 STO C STO D STO E 0.9
Execute:
EXEC FN → x = 0.9, y = 0.14394
|
| 105 |
Linear Equation Solver
Solves a system of n equations in n unknowns (n = 1..9)
Store coefficients in extended registers as follows:
a11x1 + a12x2 + … = b1 in registers R.01…R.09, with b1 in R.00
a21x1 + a22x2 + … = b2 in registers R.11…R.19, with b2 in R.10
...
Set x = number of equations
On return: Solutions x1, x2, ... in registers R1, R2, ...
|
Solve this system of 4 equations in 4 unknowns:
2x1 - 3x2 + 5x3 - x4 = 2
-5x1 + 7x2 + x3 + x4 = 6
5x1 - 4x2 - 2x3 + 8x4 = 8
11x1 + 6x2 + 5x3 -8x4 = -39
2 STO.01 -3 STO.02 5 STO.03 -1 STO.04 2 STO.00
–5 STO.11 7 STO.12 1 STO.13 1 STO.14 6 STO.10
5 STO.21 -4 STO.22 -2 STO.23 8 STO.24 8 STO.20
11 STO.31 6 STO.32 5 STO.33 -8 STO.34 -39 STO.30
4 EXEC FN ➞ x1 = -2, x2 = -1, x3 = 1, x4 = 2 (in R1..R4)
|
| 106 |
Quartic Equation (aka Biquadratic equation)
Finds all solutions of the equation ax4 + bx3 + cx2 + dx + e = 0.
Input: a..e ➞ registers A..E.
Results may be complex and are stored as follows:
x1 = R1 + RS1i, x2 = R2 + RS2i, x3 = R3 + RS3i, x4 = R4 + RS4i
x = result type (see info field of function)
|
Find the roots of x4 + x - 1 = 0:
CL REG 1 STO A STO D CHS STO E
EXEC FN
Results: x = 2, i.e. two distinct real roots and two complex conjugate non-real roots:
x1 = 0.7245, x2 = -1.2207, x3,4 = 0.2481 ± 1.0340i
Verify solution x3:
CPLX RCL 3 x2 x2 RCL+3 0 ENTER 1 – ➞ 0 + 0i
|
| 110 |
Matrix Print
Print n×n matrix stored in extended registers
Assuming the coefficients of an n×n matrix are stored in extended registers as follows:
a11x1 + a12x2 + … = b1 in registers R.01…R.09, with b1 in R.00
a21x1 + a22x2 + … = b2 in registers R.11…R.19, with b2 in R.10
...
then each row of the matrix is printed as a block of numbers.
The last number in each block is the b value.
Set x = number of rows (n)
|
With x = 2, output will typically look like this:
Row 1:
0.6709 01
0.6463 02
0.3150 00
Row 2:
0.8665 11
0.4622 12
0.2765 10
|
| 111 |
MAT –
Subtract extended registers R.91..R.99 from internal registers R1..R9
|
|
| 112 |
MAT XCH
Exchange extended registers R.91..R.99 with internal registers R1..R9
|
|
| 113 |
MAT CHS
Change sign of all values in extended registers R.91..R.99
|
|
| 115 |
Cholesky Decomposition
Perform Cholesky decomposition on 3x3 matrix formed by registers R1..R9
(where row 1 = R1..R3)
This operation replaces the original matrix A by a unique triangular matrix L, called the Cholesky factor,
such that A = LLT (LT = transpose of L).
To verify the result, perform the following operations:
MAT T 'Transpose L
MAT STO 'Store LT in R.91..R.99
MAT T 'Transpose LT to revert to L
MAT MUL 'Multiply L by its transpose LT
R1..R9 should now contain the original matrix A.
|
Find L for the matrix A:
25 15 -5
15 18 0
-5 0 11
25 STO 1 15 STO 2 -5 STO 3
15 STO 4 18 STO 5 0 STO 6
-5 STO 7 0 STO 8 11 STO 9
EXEC FN →
5 0 0
3 3 0
-1 1 3
|
| 120 |
Primality Test
Tests if the integer in x is prime. The largest prime handled reliably is 2,038,074,743.
Returns x = 1 if the value is prime, 0 otherwise.
|
78901 is prime, 78907 is not. |
| 121 |
PopCount(x)
Returns the number of 1's in the binary representation of x.
Also known as the Hamming weight of the binary number.
If x is negative, the 1's of the 2's-complement of x are counted, including the sign bit.
In this case, x is treated as a 64-bit number.
x = any integer in the range -9,999,999,999 to +-9,999,999,999.
|
13 = 1101 → 3
2017 = 11111100001 → 7
65537 = 10000000000000001 → 2
9999999999 = 1001010100000010111110001111111111 → 20
-9999999999 = 11111111111111111111111111111101101010111...
...11101000001110000000001 → 45
|
| 130 |
Geometric Mean
Geometric mean of all numbers in range of extended registers.
x = begin of range in extended registers, y = end of range in extended registers.
Returns x = geometric mean
|
What is the geometric mean of 2, 3.4, 3.41, 7, 11, 23?
Store the numbers in consecutive registers: 33,34,..38: 2 STO.33, 3.4 STO.34,...23 STO 38
33 ENTER 38 EXEC FN ➞ 5.87 |
| 131 |
Harmonic Mean
Harmonic mean of all numbers in range of extended registers.
x = begin of range in extended registers, y = end of range in extended registers.
Returns x = harmonic mean
|
What is the harmonic mean of 2, 3.4, 3.41, 7, 11, 23?
Store the numbers in consecutive registers: 33,34,..38: 2 STO.33, 3.4 STO.34,...23 STO 38
33 ENTER 38 EXEC FN ➞ 4.40 |
| 132 |
Arithmetic-Geometric Mean
Arithmetic-geometric mean M(x,y), or agm(x,y).
Returns x = geometric mean
|
Compute Gauss's constant, defined as 1/M(1,√2):
1 ENTER 2 √x EXEC FN 1/x ➞ 0.8346268 |
| 150 |
Sinc(x)
Returns the unnormalized cardinal sine function value sin(x)/x
x may be a complex number. sinc(0) = 1.
|
Examples:
sinc(0.5) = 0.9589, sinc(-1) = 0.8415
sinc(3i) = sinh(3)/3 = 3.3393
sinc(1.49+4.13i):
CPLX 4.13 ENTER 1.49 EXEC FN → 2.93–6.45i (in x,y)
|
| –150 |
Sinc(x)
Returns the normalized cardinal sine function value sin(πx)/(πx)
x may be a complex number. sinc(0) = 1.
|
Examples:
sinc(0.5) = 0.6366, sinc(-1) = 0
sinc(3i) = sinh(3π)/(3π) = 657.3973:
sinc(1.49+4.13i):
CPLX 4.13 ENTER 1.49 EXEC FN → -5766.33+14535.79i (in x,y)
|
| 152 |
LN(x!)
Returns the natural logarithm of the factorial of any positive number
0 ≤ x ≤ 4.4673259 × 1097.
|
Examples:
x = 5 → 4.7875, (e4.7875 = 120 = 5!)
Number of digits of 100,000 ! : 456,754
152 STO FN EEX 5 EXEC FN 10 LN ÷
8 STO FN x≷y EXEC FN 10x →
x = 2.8242, y = 456753 (100,000! = 2.8242 × 10456753)
|
| 153 |
LN(1+x)
High-precision evaluation, to be used with small values of x.
|
Example:
If x = e^(π * 10⁻⁹):
a. 3.141592649 × 10-9 (function result)
b. 3.141592759 × 10-9 (computed normally)
c. 3.14159264865 × 10-7 (correct result)
|
| 154 |
ex–1
High-precision evaluation, to be used with small values of x.
|
Example:
If x = e^(π * 10⁻⁹):
a. 3.141592659 × 10-9 (function result)
b. 3.140000000 × 10-9 (computed normally)
c. 3.14159265852 × 10-9 (correct result)
|
| 155 |
Lambert(x)
Returns the Lambert W function value of x.
If x = W(arg) then arg = x·ex.
arg ≥ -1/e (real values only)
If -1/e < arg < 0, two values exist; only one is returned.
|
Examples:
Lambert(0) = 0
Lambert(-1/e) = -1
Lambert(-ln(2)/2) = -ln(2)
Lambert(1) = 0.567143 (the Ω constant; Ω·eΩ = 1) |
| 160 |
Lucas(x)
Returns the Lucas number of x, defined as Φx + Φ–x·cos(π·x),
where Φ = Golden Ratio
Note: The Lucas number sequence is built in the same way as the Fibonacci number sequence, except that
it starts with 2,1,.. instead of 0,1,..
|
Examples:
Lucas(7) = 29
Lucas(-37) = -4
Lucas(π) = 4.3357
|
| 165 |
Riemann Zeta Function ζ(x)
Returns the zeta function value of x (x = real number)
Overflow if x < –118.289468.
Notes:
ζ(0) = –1/2
ζ(1) = +∞
ζ(2) = π2/6 = 1.644934067
ζ(3) = 1.202056903 (Apéry's constant)
ζ(4) = π4/90 = 1.082323234
ζ(2n) = 0 for all negative integers n
|
Examples:
ζ(0.95) = -19.42643720
ζ(1.05) = 20.58084430
ζ(π) = 1.176241738
ζ(20) = 1.000000954
ζ(-118.118) = 2.537130194E99
|
| 166 |
Bernoulli(n)
Returns the nth Bernoulli number, with x = n (integer, 0 ≤ n ≤ 117)
Overflow if n > 117.
Notes:
B(0) = 0
B(1) = ±0.5
B(2n+1) = 0 for all integers n > 0
|
Examples:
B(2) = 1/6 = 0.166666667
B(10) = 5/66 = 0.075757576
B(116) = -1.748892184E98
|
| |
Geometry |
|
| 250 |
Truncated Circular Cone
Calculates properties of the truncated circular cone. For the regular cone, set top radius to zero.
Inputs: x = base surface radius, y = top surface radius (0 for regular cone),
z = height
Returns: x = volume, y = total surface, z = lateral surface, t = center of mass (above base surface)
|
Calculate properties of a truncated cone with height h = 7, base radius r1 = 5 and top radius r2 = 2:
7 ENTER 2 ENTER 5
EXEC FN ➞
285.88 (volume), 258.59 (total surface), 167.48 (lateral surface), 2.56 (center of mass)
|
| 251 |
Spherical Segment or Cap
Calculates properties of the spherical segment. For the spherical cap, set top radius to zero.
Inputs: x = lower radius of segment, y = upper radius of segment (0 for cap),
z = height of segment
Returns: x = volume, y = total surface, z = lateral surface (or cap surface), t = radius of sphere
|
Calculate properties of a spherical segment with height
h = 7, base radius r1 = 5 and top radius r2 = 2:
7 ENTER 2 ENTER 5
EXEC FN ➞
498.47 (volume), 327.96 (total surface), 236.85 (lateral surface), 5.39 (radius of sphere)
|
| |
Physics |
|
| 300 |
Oblique Throw (meters)
Calculates the ballistic trajectory of an object thrown at a given initial angle and initial velocity.
Inputs: RA = initial angle, RB = initial velocity, x = desired horizontal distance
Returns:
x = height at distance x
y = maximum height (at half of landing point distance)
z = distance of landing point
t = time to reach highest point
|
A ball is thrown at at angle of 65 degrees. The initial velocity is 20 m/s.
Find the maximum height, the time to reach it, the height at horiz. distance = 7 m, and the distance of the landing point.
65 STO A 20 STO B 7 EXEC FN ➞
11.65 m (height at horiz. dist. 7 m), 16.75 m (max. height), 31.25 m (distance of landing point), 1.85 s (time to reach highest point)
|
| –300 |
Oblique Throw (feet)
See description above |
A ball is thrown at at angle of 65 degrees. The initial velocity is 50 ft/s.
Find the maximum height, the time to reach it, the height at horiz. distance = 20 ft, and the distance of the landing point.
65 STO A 50 STO B 20 EXEC FN ➞
28.48 ft (height at horiz. dist. 20 ft), 31.91 ft (max. height), 59.52 ft (distance of landing point), 1.41 s (time to reach highest point)
|
| 305 |
Satellite I
Properties of a satellite at known altitude
Input:
x = altitude above Earth surface, in m
Returns:
x = orbital time, in s
y = velocity, in m/s
z = velocity, in km/h
t = escape velocity, in m/s
(minimum speed needed to escape from Earth's gravitational influence)
|
Calculate properties of a satellite 640 km above Earth.
640 EEX 3 EXEC FN ➞
5842 s ≈ 97 min (orbital time)
7541 m/s (velocity)
27147 km/h (velocity)
10664 m/s (escape velocity)
|
| –305 |
Satellite II
Properties of a satellite with known orbital time
Input:
x = orbital time around Earth, in s
Returns:
x = altitude above Earth surface, in m
y = velocity, in m/s
z = velocity, in km/h
t = escape velocity, in m/s
(minimum speed needed to escape from Earth's gravitational influence)
|
Calculate properties of a synchronous satellite.
Orbital time = 1 day = 86400 s
86400 EXEC FN ➞
35873006 m ≈ 35.9 km (altitude)
3072 m/s (velocity)
11059 km/h (velocity)
4345 m/s (escape velocity)
|
| 310 |
Hydrogen Atom I
Calculates properties of an electron in orbit number n
(n = "principal quantum number")
Input:
x = orbit no.(1,2,3,..)
Returns:
x = total energy of electron (potential and kinetic), in eV
y = radius of orbit, in m
z = velocity of electron, in m/s
t = orbital frequency (revolutions per second), in Hz
|
Calculate the electron properties in the third orbit.
3 EXEC FN ➞
-1.5117 eV (energy)
4.7626·10-10 m (radius)
7.2923·105 m/s (velocity)
2.4369·1014 Hz (frequency)
To convert the energy from eV into J, select the built-in constant 01 ("e", "Elementary charge") and multiply.
|
| –310 |
Hydrogen Atom II
Calculates energy emitted when electron drops to lower orbit
Inputs:
x = lower orbit number, y = higher orbit no. (1,2,3,..)
Returns:
x = energy of photon emitted, in eV
y = frequency of photon emitted, in Hz
z = energy of photon emitted, in J
t = wavelength of photon emitted, in nm
|
Calculate wavelength and energy of photon emitted when the electron drops from orbit 6 to orbit 1.
6 ENTER 1 EXEC FN ➞
13.2278 eV (energy)
3.1985·1015 Hz (frequency)
2.1193·10-18 J (energy)
93.7303 nm (wavelength)
|
| |
Electrical Engineering |
|
| 400 |
Resistance
Equivalent resistance of parallel resistors stored in R.x..R.y.
x = begin of range in extended registers, y = end of range in extended registers.
Returns 0 if any value in the range is 0.
|
What is the resistance of 1, 2, 3, 4, 5 Ω wired in parallel?
Store 1,2,3,4,5 in registers 20,21,22,23,24: 1 STO.20, 2 STO.21,...
400 EXEC FN ➞ 0.44 Ω |
| 401 |
RLC Circuit (series)
Calculates impedances and phase shift of an series RLC circuit.
Input:
R0 = frequency (in Hz), R1 = resistor (in Ω), R2 = inductor(in H)
R3 = capacitor (in F)
[To omit a component, set its value to 0.]
Returns:
x = total impedance (in Ω)
y = inductive impedance (in Ω)
z = capacitive impedance (in Ω)
t = phase shift between voltage and current (in current angular units)
R4 = resonant frequency (in Hz)
|
Calculate values for a series RLC circuit consisting of a resistance of 12 Ω,
an inductance of 0.15 H and a capacitor of 100 µF connected to a 50 Hz power supply.
50 STO 0 12 STO 1 0.15 STO 2 100 EEX CHS 6 STO 3
EXEC FN ➞
x = 19.44 Ω (total impedance)
y = 47.12 Ω (inductive reactance)
z = 31.83 Ω (capacitive reactance)
t = 51.88 ° (phase shift in degrees)
R4 = 41.09 Hz (resonant frequency)
Set frequency to resonant frequency and observe total impedance:
RCL 4 STO 0 EXEC FN ➞ 12.00 (= resistance value)
|
| –401 |
RLC Circuit (parallel)
Calculates impedances and phase shift of a parallel RLC circuit.
Input:
R0 = frequency (in Hz), R1 = resistor (in Ω), R2 = inductor(in H)
R3 = capacitor (in F)
[To omit a component, set its value to a negative number.]
Returns:
x = total impedance (in Ω)
y = inductive impedance (in Ω)
z = capacitive impedance (in Ω)
t = phase shift between voltage and current (in current angular units)
R4 = resonant frequency (in Hz)
|
Calculate values for a parallel RLC circuit consisting of a resistor of 50 Ω,
a coil of 20 mH and a of 5 µF capacitor connected to a 100 Hz power supply.
100 STO 0 50 STO 1 20 EEX CHS 3 STO 2 5 EEX CHS 6 STO 3
EXEC FN ➞
x = 12.66 Ω (total impedance)
y = 12.57 Ω (inductive reactance)
z = 318.31 Ω (capacitive reactance)
t = -75.34 ° (phase shift in degrees)
R4 = 503.29 Hz (resonant frequency)
Set frequency to resonant frequency and observe total impedance:
RCL 4 STO 0 EXEC FN ➞ 12.00 (= resistance value)
|
| 402 |
Wye-Delta Transformation
Converts star configuration of three impedances into its equivalent triangle configuration.
Real impedances: input values in R1, R2, R3. Output values replace input values.
Complex impedances: input values in R1, R2, R3 (real parts) and RS1, RS2, RS3 (imaginary parts).
Output values replace input values.
|
Convert values 43.35 Ω, 1.57 Ω, 81.98 Ω, arranged in star configuration, into values for the equivalent triangle configuration.
43.35 STO 1 1.57 STO 2 81.98 STO 3
EXEC FN ➞ R1 = 86.52 Ω, R2 = 2388.92 Ω, R3 = 45.75 Ω |
| –402 |
Delta-Wye Transformation
Converts triangle configuration of three impedances into its equivalent star configuration.
Real impedances: input values in R1, R2, R3. Output values replace input values.
Complex impedances: input values in R1, R2, R3 (real parts) and RS1, RS2, RS3 (imaginary parts).
Output values replace input values.
|
Convert values 50+12i Ω, 75-3.1i Ω, 100+11i Ω, arranged in triangle configuration, into values for the equivalent star configuration.
CPLX 12 ENTER 50 STO 1 -3.1 ENTER 75 STO 2
11 ENTER 100 STO 3
EXEC FN ➞ R1 = 33.43-0.67i Ω, R2 = 22.15+5.82i Ω,
R3 = 16.99+1.81i Ω
Note that in complex mode, PrintX prints both real and imaginary parts. |
| |
Astronomy |
|
| 650 |
Gregorian Date ⇢ Julian Date
Shows Julian date of a given Gregorian date.
Input:
x = date (mm.ddyyyy)
Date may be in the range Jan 1, 0001 to Dec 31, 9999.
If an invalid date is given, the current date is used.
Dates before Oct 5, 1582 remain unchanged.
Non-existing Gregorian dates will produce an error (Oct 5, 1582 to Oct 14, 1582).
Returns:
x = Julian date
|
Isaac Newton was born on Jan 4, 1643 (Gregorian calendar).
What is his birthday according to the calendar in use back then?
1.041643 EXEC FN ➞ 12.251642 (Dec 25, 1642)
What is today's Julian date (if today = Nov 16, 2017)?
0 EXEC FN ➞ 11.032017 (Nov 11, 2017)
|
| –650 |
Julian Date ⇢ Gregorian Date
Shows Gregorian date of a given Julian date.
Input:
x = date (mm.ddyyyy)
Date may be in the range Jan 1, 0001 to Oct 19, 9999.
If an invalid date is given, the current date is used.
Dates before Oct 5, 1582 remain unchanged.
Returns:
x = Gregorian date
|
What are the Gregorian dates of Julian dates Oct 4 and 5, 1582?
10.041582 EXEC FN ➞ 10.041582 (Oct 4, 1582)
10.051582 EXEC FN ➞ 10.151582 (Oct 15, 1582)
What is the Gregorian date if today's date is interpreted as Julian date (assuming today = Nov 16, 2017)?
0 EXEC FN ➞ 11.292017 (Nov 29, 2017)
|
| 651 |
Calendar Date to Julian Day Number
Calculates the Julian day number from a given date and time.
Input:
x = date (mm.ddyyyy)
y = time (hh.mmss)
Date may be in the range Jan 1, 0001 to Dec 31, 9999.
If an invalid date is given, the current date is used; an invalid time will be changed to the current time.
Dates after Oct 4, 1582 are assumed to be Gregorian.
Non-existing Gregorian dates will produce an error (Oct 5, 1582 to Oct 14, 1582).
Returns:
x = Julian day number (negative if input date after Oct 4, 1582 was entered as Julian date, i.e. negative)
y = time
|
What is the Julian day number of July 4, 1776?
To get the integer value, set time to noon.
12 ENTER 7.041776
EXEC FN ➞ 2369916
Calculate the Julian day number of the current date and time:
-1 ENTER ENTER (Set invalid date and time)
EXEC FN ➞ 2458071.918
x≷y ➞ 10.02188 (time)
|
| –651 |
Julian Day Number to Calendar Date
Calculates the calendar date corresponding to a given Julian day.
Input:
x = Julian date number (negative to enforce Julian calendar)
Julian day number may be in the range 1,721,423.5 to 5,373,484.5.
The fractional part denotes the deviation from noon, i.e. x.5 is 0:00 of day x+1.
Returns:
x = date (negative if date after Oct 4, 1582 is shown as Julian date)
y = time
|
On what date was Julian day number 2,000,000?
2 EEX 6 EXEC FN ➞ 9.140763 (Sep 16, 763)
What dates correspond to Julian day numbers 2,299,160 and 2,299,161?
2299160 EXEC FN ➞ 10.041582 (Oct 4, 1582)
2299161 EXEC FN ➞ 10.151582 (Oct 15, 1582)
[Note change from Julian calendar to Gregorian calendar]
|
| 655 |
UT to GMST
Converts universal time to Greenwich mean sidereal time.
Input:
x = universal time UT (hh.mmss)
y = date (mm.ddyyyy)
If an invalid date or time is given, the current value is used.
Non-existing Gregorian dates will produce an error (Oct 5, 1582 to Oct 14, 1582).
Returns:
x = Greenwich mean sidereal time GMST (hh.mmss)
y = Greenwich mean sidereal time GMST (° decimal)
z = Time (hh.mmss), input UT or current time if invalid
t = Date (mm.ddyyyy), input date or current date if invalid |
What was the GMST at 14h 36m 51.67s UT on April 22nd 1980?
4.221980 ENTER 14.365167
EXEC FN ➞ 4.400523 (4h 40m 5.23s) or 70.0218° (in Y)
Find the GMST at 6h 30m UT on Oct 3, 2001.
10.032001 ENTER 6.30
EXEC FN ➞ 7.180833 (7h 18m 8.33s) or 109.5347° (in Y)
Find the GMST if the UT is the current time and date.
-1 ENTER EXEC FN ➞ UT, R↑ ➞ date, R↑ ➞ time
|
| –655 |
GMST to UT
Converts Greenwich mean sidereal time to universal time.
Input:
x = Greenwich mean sidereal time (hh.mmss)
y = date (mm.ddyyyy)
If an invalid date or time is given, the current value is used.
Non-existing Gregorian dates will produce an error (Oct 5, 1582 to Oct 14, 1582).
Returns:
x = universal time UT (hh.mmss)
y = universal time UT (° decimal)
z = Time (hh.mmss), input GMST or current time if invalid
t = Date (mm.ddyyyy), input date or current date if invalid |
What was the UT at 4h 40m 5.23s GMST on April 22nd 1980?
4.221980 ENTER 4.400523
EXEC FN ➞ 14.3651673 (14h 36m 51.67s) or 219.2153° (in Y)
Find the UT at 7h 18m 8.33s UT on Oct 3, 2001.
10.032001 ENTER 7.180833
EXEC FN ➞ 6.30000 (6h 30m) or 97.5000° (in Y)
Find the UT if the GMST is the current time and date..
-1 ENTER EXEC FN ➞ UT, R↑ ➞ date, R↑ ➞ time
|
| |
Surveying |
|
| 700 |
Geodesic Distance
Calculate distance between two locations on Earth, taking into account the Earth's flattening (based on WGS-84 values).
Input (all angles in H.MS format):
x = latitude 2
y = longitude 2
z = latitude 1
t = longitude 1
(use minus sign to differentiate between East/West and North/South)
Returns:
x = geodesic distance (in km)
y = geodesic distance (in mi)
z = geodesic distance (in nmi)
|
Calculate the geodesic distance between the Observatoire de Paris (France) and the
U.S. Naval Observatory at Washington (D.C.), using the following coordinates:
Paris: longitude 2°20'14" East, latitude 48°50'11" North
Washington: longitude 77°03'56" West, latitude 38°55'17" North
2.2014 ENTER 48.5011 ENTER
77.0356 CHS ENTER 38.5517
EXEC FN ➞ 6181 km (= 3841.08 mi = 3337.81 nmi) |
| |
Business |
|
| 800 |
NOM2EFF
Converts nominal annual interest x (in %) rate to effective rate, using y periods. |
Compute effective annual rate if nominal annual interest of 6.0% is compounded quarterly:
4 ENTER 6
EXEC FN ➞ 6.14% (effective annual rate) |
| –800 |
EFF2NOM
Converts effective annual interest x (in %) rate to nominal rate, using y periods. |
Compute nominal annual interest if effective annual rate of 7.7%, compounded monthly, is known:
12 ENTER 7.7
EXEC FN ➞ 7.44% (effective annual rate) |
| 801 |
Rule of 78's
Interest portion and interest rebate of a finance charge
x = periodic payment number, y = total periods, z = finance charge
Returns: x = interest portion of the xth payment, y = rebate |
Calculate interest portion and rebate of the 25th payment of a 30-month loan having a finance charge of $180.
180 ENTER 30 ENTER 25 EXEC FN ➞ 2.32 (interest portion) x≷y ➞ 5.81 (rebate) |
| 810 |
Bond Price
Given x = decimal annual coupon rate (in %), y = annual yield to maturity (in %), z = days between purchase and maturity), calculates bond price
|
What is the price of a 4% bond yielding 3% and maturing in 99 days?
99 ENTER 3 ENTER 4 EXEC FN ➞ 100.27
|